1、通过二次函数图像法、均值不等式法和函数导数法,介绍已知当0<x<1时,求函数y=x(1-x)的最大值的主要步骤。
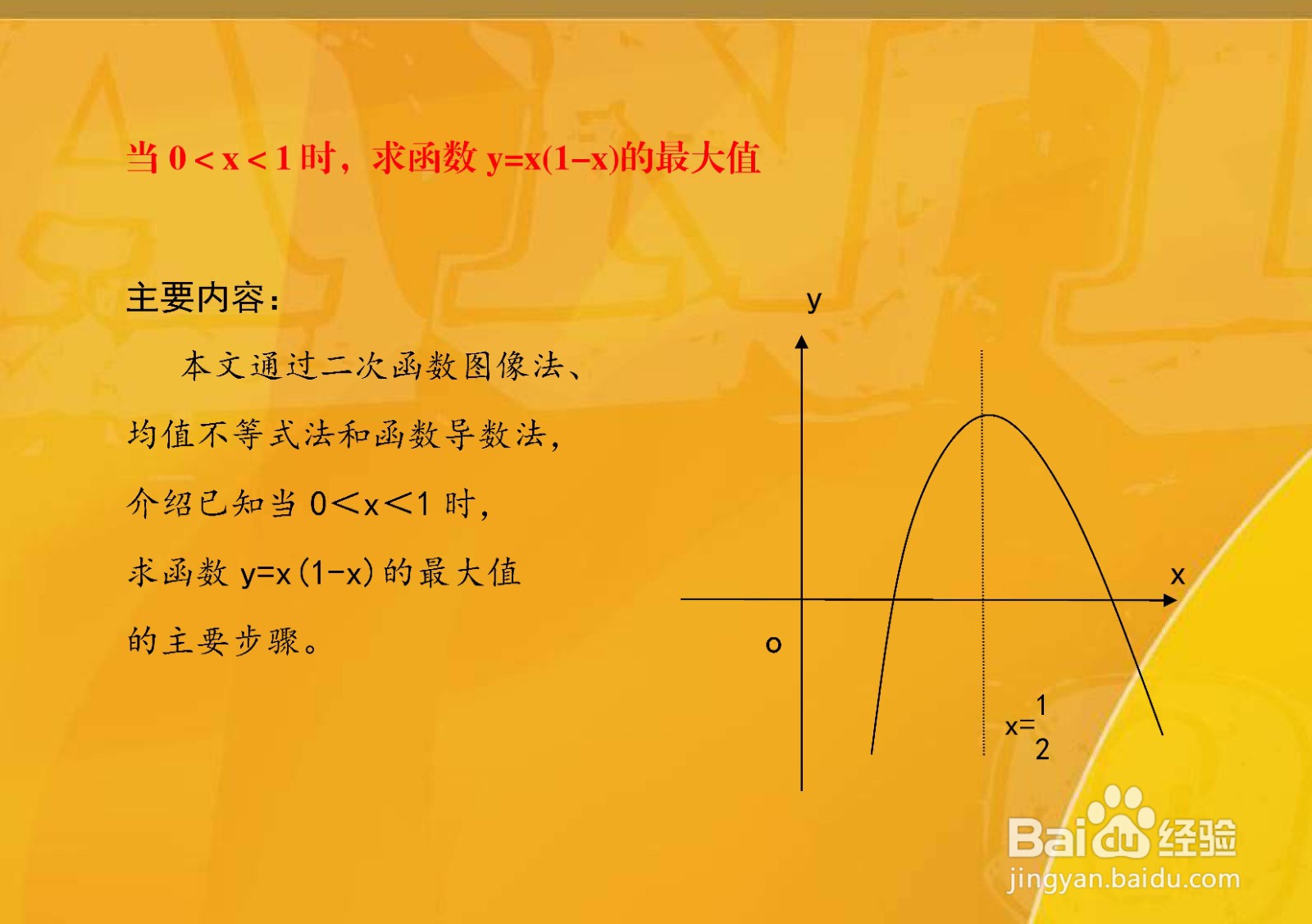
2、因为y=x(1-x),所以y=x-x^2=-x^2+x,
其对称轴x=b/2a=-1/2*(-1)=1/2∈(0,1),
该二次函数的开口向下,所以在对称轴处取得最大值,则:
ymax=f(1/2)
=(1/2)*(1-1/2)
=1/4.

3、由不等式ab≤(a+b)^2,a,b∈R+知:
y=x(1-x)
≤{[x+(1-x)]/2}^2
=( 1/2)^2=1/4.

4、计算函数的一阶导数,判断函数的单调性,进而求出函数的最大值。

5、∵y=x(1-x),∴y=x-x^2,对x求导有:
dy/dx=1-2x,令dy/dx=0,则:
1-2x=0,此时x=1/2,且有:
(1) 当x∈(0,1/2)时,dy/dx>0,函数为增函数;
(2) 当x∈[1/2,1)时,dy/dx≤0,函数为减函数。
则当x= 1/2时,y取最大值,此时ymax=1/4。