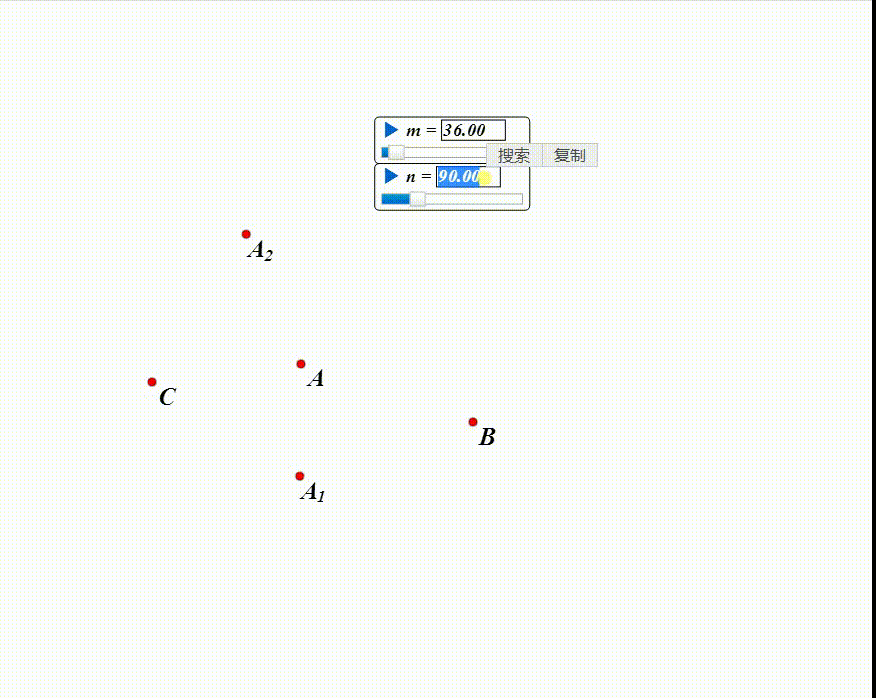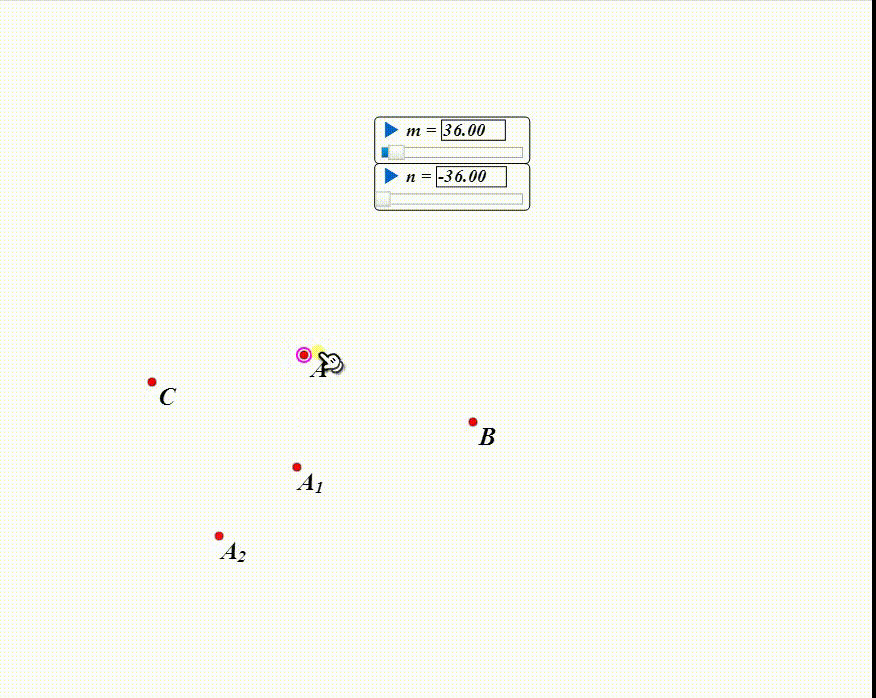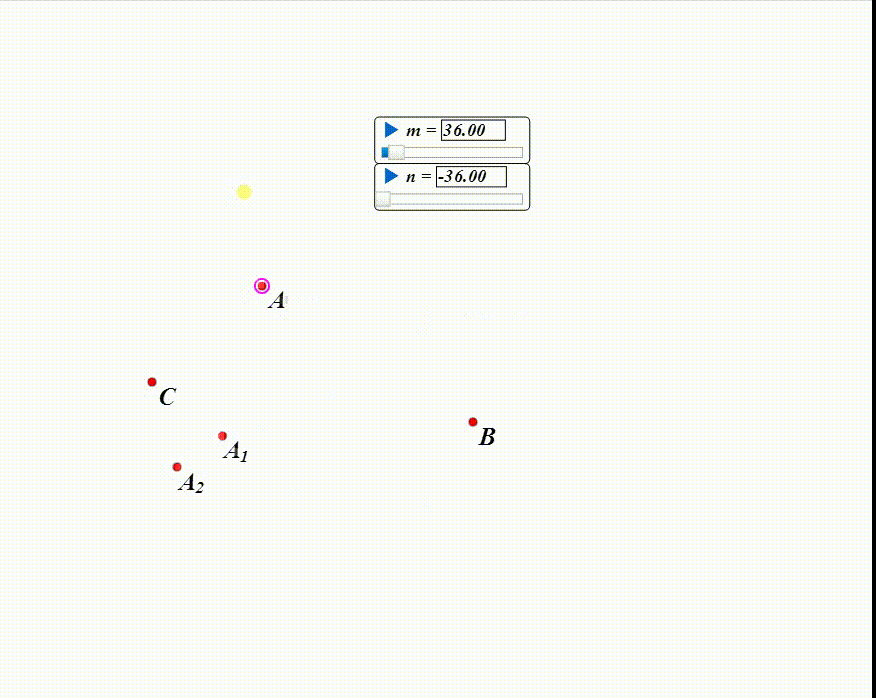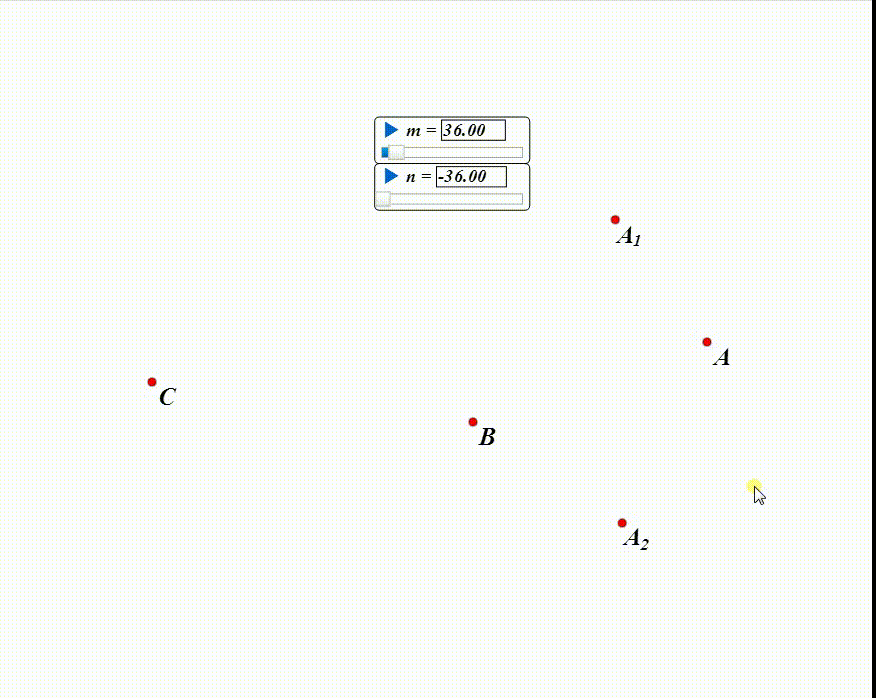
1、用网络画板演示:
设A绕B旋转m,得到A1;
A1绕C旋转n,得到A2。
在平面上拖动A,看A有没有可能和A2重合。

2、如果A和A2在某个位置可以重合,那么这就不是平移。

3、如果m+n=0,那么A到A2就是一个平移,A与A2不可能重合。
1、用Mathematica分析:
设A={x,y}
A是平面上的自由点。
A绕B——{a,b}——旋转m,得到A1。

2、A1绕C——{c,d}——旋转n,得到A2。

3、什么时候,u[r[A]]代表平移呢?
只要(A2=u[r[A]])-A与A无关就行了。

4、需要:
x (-1 + Cos[m + n])--y Sin[m + n]=0
y (-1 + Cos[m + n])+x Sin[m + n]=0
这个方程组对任意实数对{x,y}都成立。
观察发现,当Cos[m + n]=1的时候,就满足要求。
此时,可以限定m+n=0.
