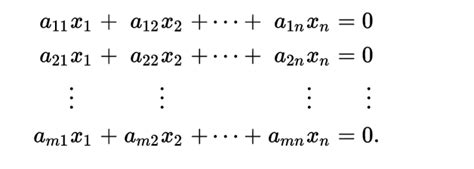
首先,你说反了。齐次线性方程组中,如果D≠0,则只有零解;如果有非零解,则系数行列式D=0。
这两个部分互为逆否命题,如果前半部分成立,则后半部分必然成立。
∵齐次线性方程组的常数项全为0,∴Dj=0
又∵D≠0
∴解xj=Dj/D=0,即所有解均等于0,即全为0解
这就证明了前半部分成立,因此后半部分也成立。
就是解不等于0。

齐次线性方程组,指常数项全部为零的线性方程组。
基本性质:
1.齐次线性方程组的两个解的和仍是齐次线性方程组的一组解。
2.齐次线性方程组的解的k倍仍然是齐次线性方程组的解。
3.齐次线性方程组的系数矩阵秩r(A)=n,方程组有唯一零解。
4.齐次线性方程组的系数矩阵秩r(A)<n,方程组有无数多解。
5. n元齐次线性方程组有非零解的充要条件是其系数行列式为零。
齐次线性方程组与非齐次线性方程组的区别:齐次的没有常数项,就是AX=0,非齐次的有常数项,就是AX=B。